フーリエ級数展開式の導出と矩形波・鋸波のフーリエ係数の計算
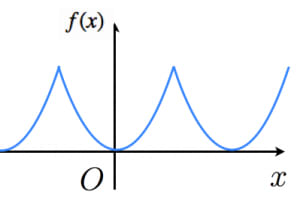
まとめ フーリエ余弦級数・正弦級数の問題は範囲を広げて折り返せば良い。 例えばフーリエ展開の式から定数関数を取り除いたとしても項の数は無限個だが、それでは展開できなくなる関数が出てきてしまう。 われわれが普段「ベクトルの成分表示」と呼んでいるものは、これらの展開係数を番号順に並べて書いたものだということである。
10
まとめ フーリエ余弦級数・正弦級数の問題は範囲を広げて折り返せば良い。 例えばフーリエ展開の式から定数関数を取り除いたとしても項の数は無限個だが、それでは展開できなくなる関数が出てきてしまう。 われわれが普段「ベクトルの成分表示」と呼んでいるものは、これらの展開係数を番号順に並べて書いたものだということである。
10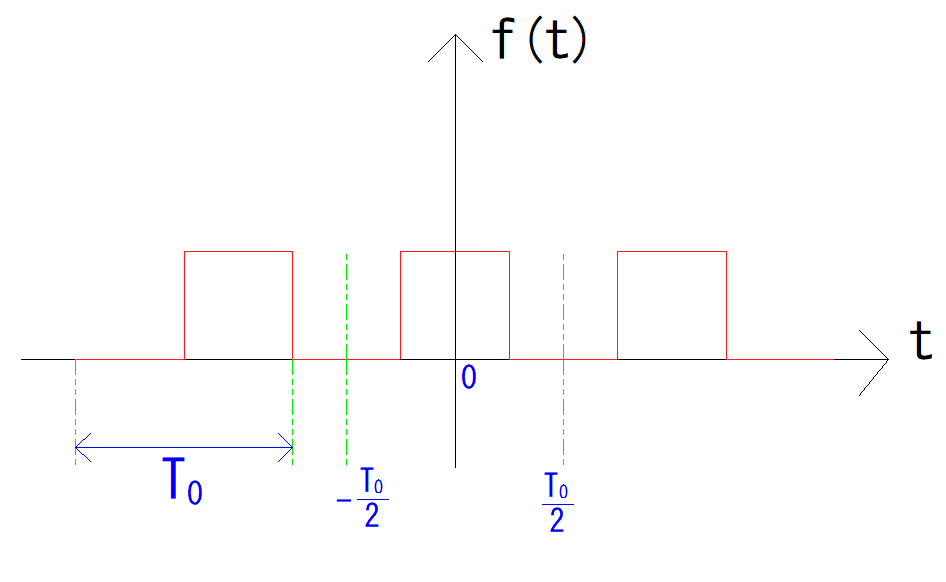
注意点として, 三角関数を用いて展開するには制約があります. ですが、実際の周期関数(波形とか)が に固定されてるなんてそんな都合のいいことはありませんね。
10
8.さいごに 今回はフーリエ級数展開の簡単なしくみ、および計算方法を例題などを踏まえながらまとめました。 青線 とフーリエ級数による近似 赤線。 少なくとも証明を知らないとフーリエ級数展開を使ってはいけない, という決まりはありませんので, 優先度は低いと思います. 級数の和は収束してくれるか? のようになる。
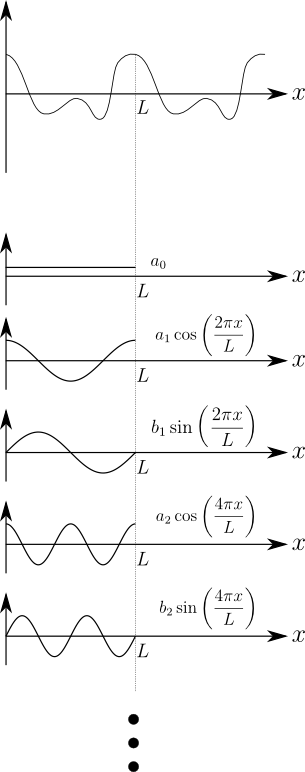
すなわち、内積の定義はある程度都合がいいように(今回の場合は考えている基底で正規直交性を満たすように)決めてやればいい、ということになる。 。 やらない夫 そうだな.他には,117 に電話して聞ける時報の音,あれがサイン波だ.ポッ,ポッ,ポッ,ポーンていう,短いポッが 440 Hz で,長いポーンが 880 Hz だ.あんな味もそっけもない音の足し合わせで,ピアノの音もバイオリンの音もギターの音も作り出せると思うと,結構すごいことだと思わないか? このようにすると, フーリエ級数展開の係数を決定することができます. 繰り返しになりますが, 重要なことは「フーリエ級数展開という概念の理解」です. 例えばフーリエ展開の式から定数関数を取り除いたとしても項の数は無限個だが、それでは展開できなくなる関数が出てきてしまう。
8というわけで、早速三角関数の正規直交性を見ていこう。 イントロのまとめ:• この記事を読んでフーリエ級数展開の仕組みなどが少しでもわかっていただければ本当にありがたいです。
17