中 点 連結 定理。 中点連結定理について詳しく解説！【問題付き】

中点連結定理とは？証明、定理の逆や応用、問題の解き方

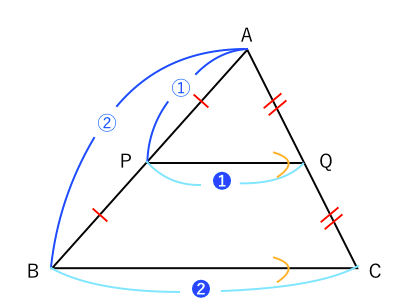
「中点連結. 3 四角形ＰＱＲＳがひし形になるとき• そのため、 中点連結定理を利用することによってMNの長さを計算できます。

18

中点連結定理とは？証明、定理の逆や応用、問題の解き方

中点連結定理とはなんだっけ？ こんにちは！この記事を書いてる Kenだよ。 逆 中点連結定理は、三角形の2つの性質を含んでいる。 数学的には、相似な図形の性質、成立条件を含め、あらゆる相似に関する定理はこの 中点連結定理 とそのを繰り返し用いることで導かれるものであるため、これでは循環論法となって、教科書に証明として記載されている一連の記述は誤りである。

中点連結定理とは

スマホ・PCどちらでも見やすいイラストで解説しているので、非常にわかりやすい内容です。 また、点Fは辺ACの中点であり、点Gは直線BCと直線DFの交点である。

1

中点連結定理と相似：定理の逆や平行四辺形の証明、応用問題の解き方

中点連結定理を使う問題は高校入試でもたまに出題されています。 おわりに. Contents• 相似の三角形では、底辺が平行な場合だと、辺の比に応じて長さの計算が可能です。 中点連結定理を用いた証明問題、長さを求める問題などです。

12

中点連結定理とは？証明、定理の逆や応用、問題の解き方

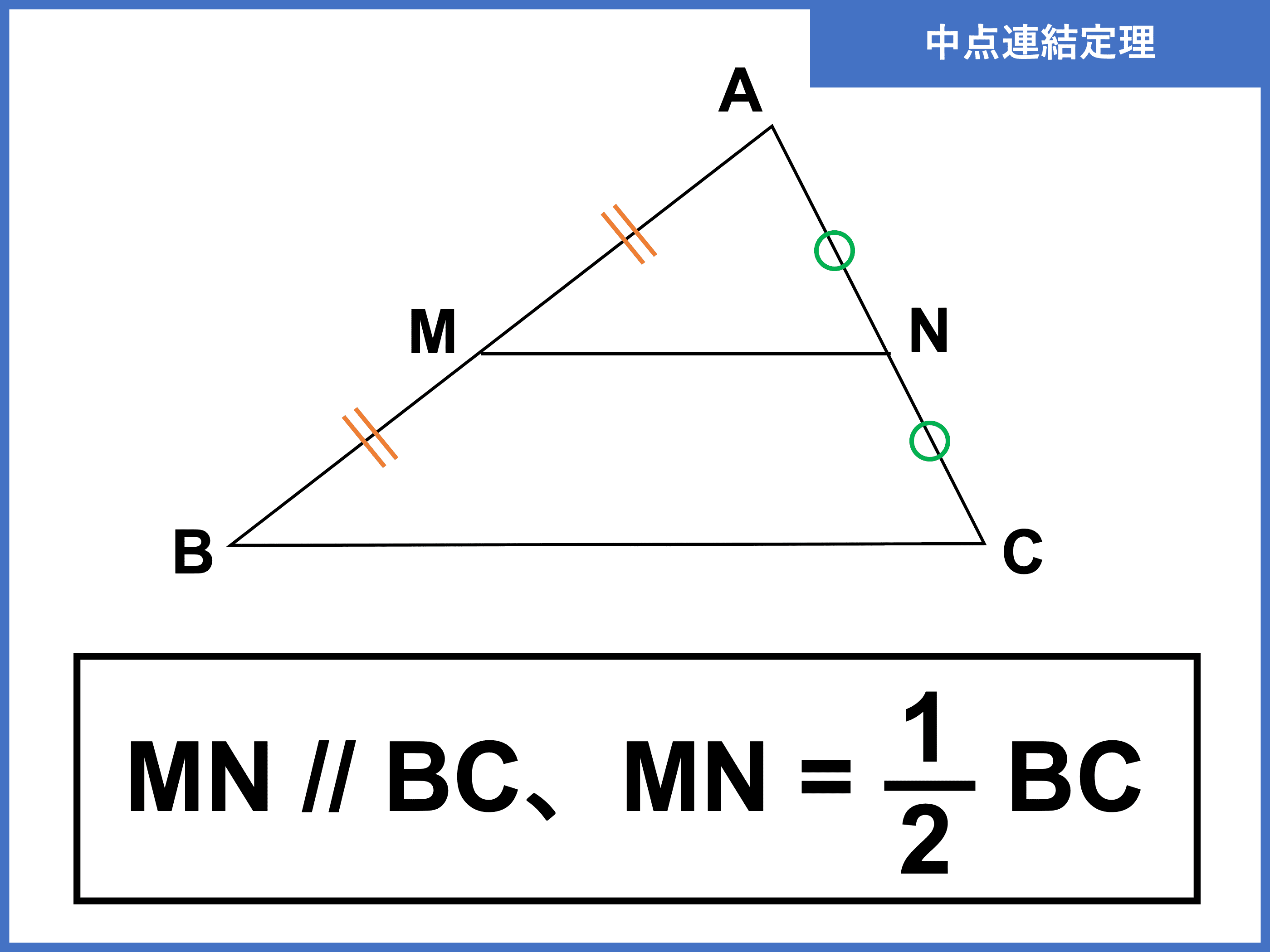
教科書対応もあり学校の授業の予習・復習にも。 図は例で、任意の二辺の中点を結んだ線と、他の一辺について、必ず上記の関係が成り立つという定理である。

中学３年数学練習問題 中点連結定理/図形と相似

- 小学生・中学生が勉強するならスクールTV。 また2つの線が平行な場合、辺の比はすべて同じになります。 この問題のようにM,Nが予めAB,ACの中点であることがわかって. このとき、四角形EFGHが平行四辺形であることを、以下のように証明した。

12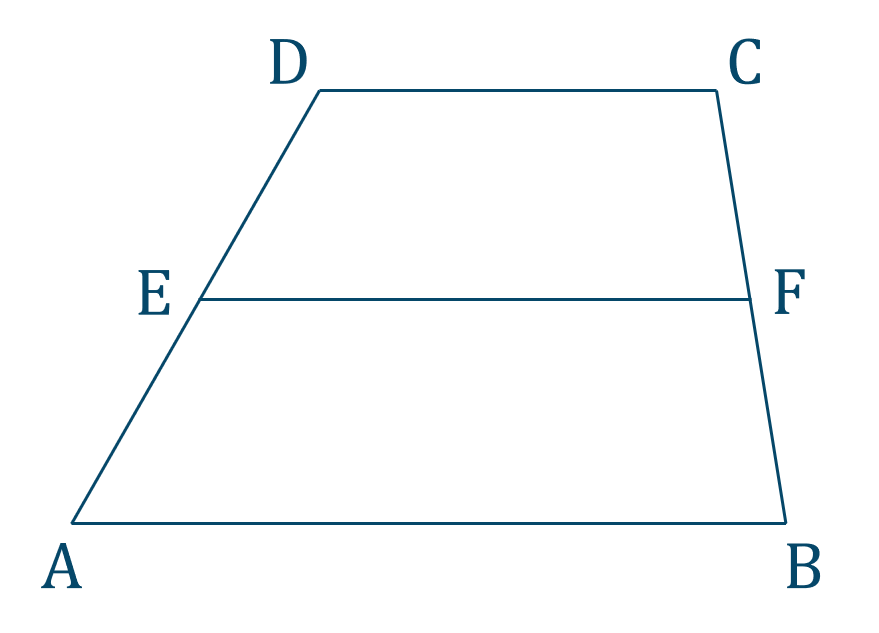

中点連結定理の証明

普段の家庭学習や定期テスト・受験勉強に！•。 （一部改題） 直感的に次のように考えたのですが. の内容であり、より簡単に「三角形の底辺を除く一辺の中点から、底辺の平行線を引くと、残りの辺の中点を通る」と表現される。

4

中点連結定理と相似：定理の逆や平行四辺形の証明、応用問題の解き方

よってすべての辺の長さが同じであるという特徴を持ちます。 これは、学習課程の便宜から、証明として用いられている方法であり、相似の性質を利用して示す特殊な例として扱われている。 AF＝GFよりFはAGの中点、AD＝CGとBG＝CG＋BCより、BG＝AD＋BCといえます。