トレミーの定理。トレミーの定理とその証明。向かい合う2組の辺と対角線の関係性｜アタリマエ！

コラム角の和と差と弦の長さ

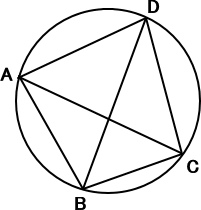
図形の証明には、図形そのものの性質だけを組み合わせて行う場合以外に、いろいろな方法がある。というわけで、答えが出ました。どのような場面において使えるか、具体的な話をすると、円に四角形が内接しており、さらに対角線が施されていたら、トレミーの定理を使えないかどうか疑ってみる価値があるといえます。

）である。（平成２７年６月１日付け）初等幾何で重要なトレミーの定理。

三角比を利用した証明の方が計算だけで済むので導くには楽かもしれません。

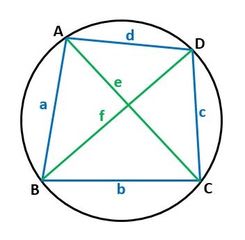
対角線の数＝７C２＝21本である。とはいえ誰かがとっくに見つけている証明だろうと思いますが．．．。

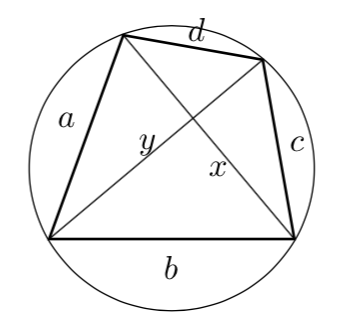
中学生ができる証明方針高校生が三角比を使って証明するのは普通です。（平成２７年６月２日付け）以下、トレミーの定理を使わない場合の解答例です。円に内接する四角形の場合不等式が等号で成立し，トレミーの不等式はと一致します。

この式を、頂点Ａ、Ｂ、Ｃ、Ｄを用いて書き直せば、プトレマイオスの定理ＡＣ・ＢＤ＝ＡＢ・ＣＤ＋ＡＤ・ＢＣが得られる。（追々記）最近、の応用題で、トレミーの不等式なるものを用いた。