円錐体積の求め方

【中1数学】円柱・円すいの体積の求め方がサクッとわかる

$の円錐求め方体積$

S：つまり、ｋ＝１／３ということですね。コレに当てはめて考えていきましょう。いったいどうすればよいでしょうか？ポイントになるのは三平方の定理中学3年生で学. 表面積は、扇形の面積と、底面の円の面積を足すだけです。

この立体の体積を求めよ。使う変数は、tyokkei（底辺の直径）、takasa（円錐の高さ）、taiseki（円錐の体積）の以上3個の実数型変数とする。しかし、「全体から一部を引く」というのを覚えておくと良いです。

用語の確認のために図を書いていませんが、『母線』とは円錐の頂点から底面の円周上に引いた線分のことです。

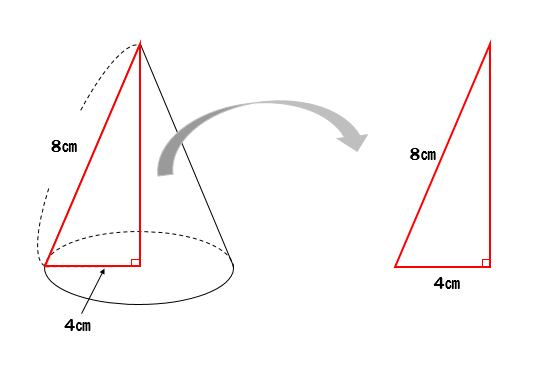
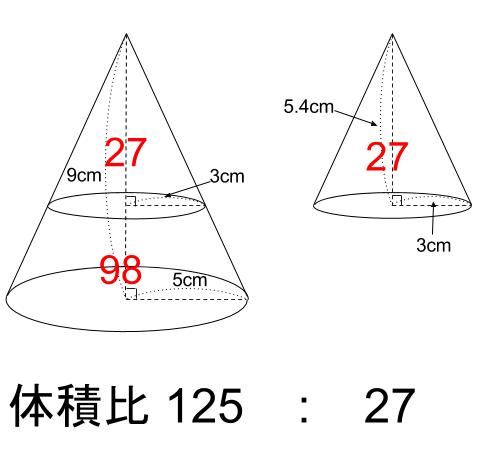
さらに「扇形の弧の長さ」が「底面の円周」と等しいことに着目すると、以下のようになります。 T：つまり、ｃがａに対して何倍になっているのかで、１／２か、１／３か、２／３かが決まるということです。だけど、コイツを円周上に回転させて移動させると、円柱ができちゃうんだ！！線分ABは円柱を産んだわけだ。

扇部分の半径母線・弧の長さを求める扇の中心角を求める問題になる• 覚えいるけどミスをする人もいます。。

まずは公式を暗記して頂き、余裕がある方は証明方法も勉強しましょう。積分って何？と興味を持ってくれた方のために、計算式だけお見せしますね（肝心なのは体積や積分といった概念ですが…）。図からこの部分だとわかります。

すごい。円錐の表面積の公式は便利なのでぜひ覚えておいてください！いかがでしたか？円錐の体積・表面積の求め方に関する解説は以上になります。

柱体と錐体の体積の求め方です。以上より、円錐の底面積と側面積を求めることができました。

Contents• ｙ＝ｘ 2の面積は正方形の１／３なんだ。となります。