ベクトル の 成分。 平面ベクトルの成分表示とその解き方

【線形空間編】基底と次元と成分

ベクトルはここまで図形的な処理をしていましたが、グラフ上にベクトルを書いて、もう少し、数式的な処理をすることができます。 定義されない演算 [ ] 以下のような計算は定義されないため実行してはならない。

9

平面ベクトルの成分表示

正方行列でない行列に対して行列式を考える理論も存在する。

6

【ゲーム数学】ベクトルの基礎

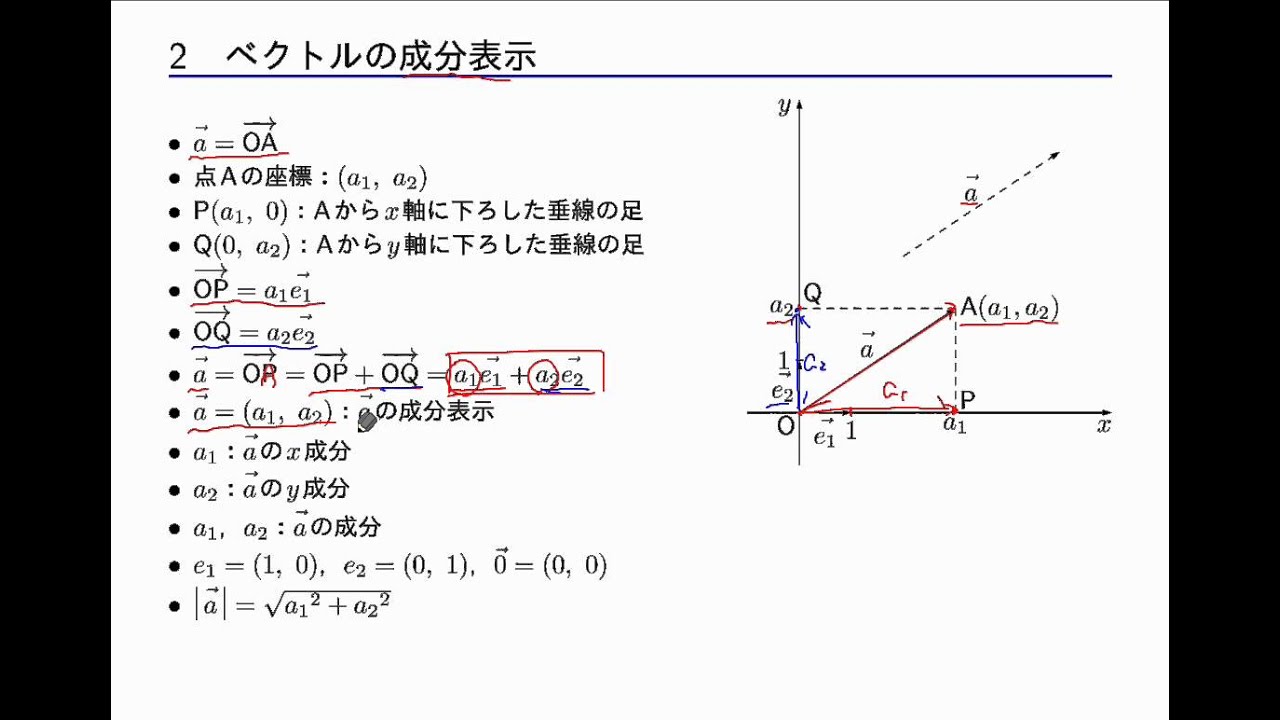
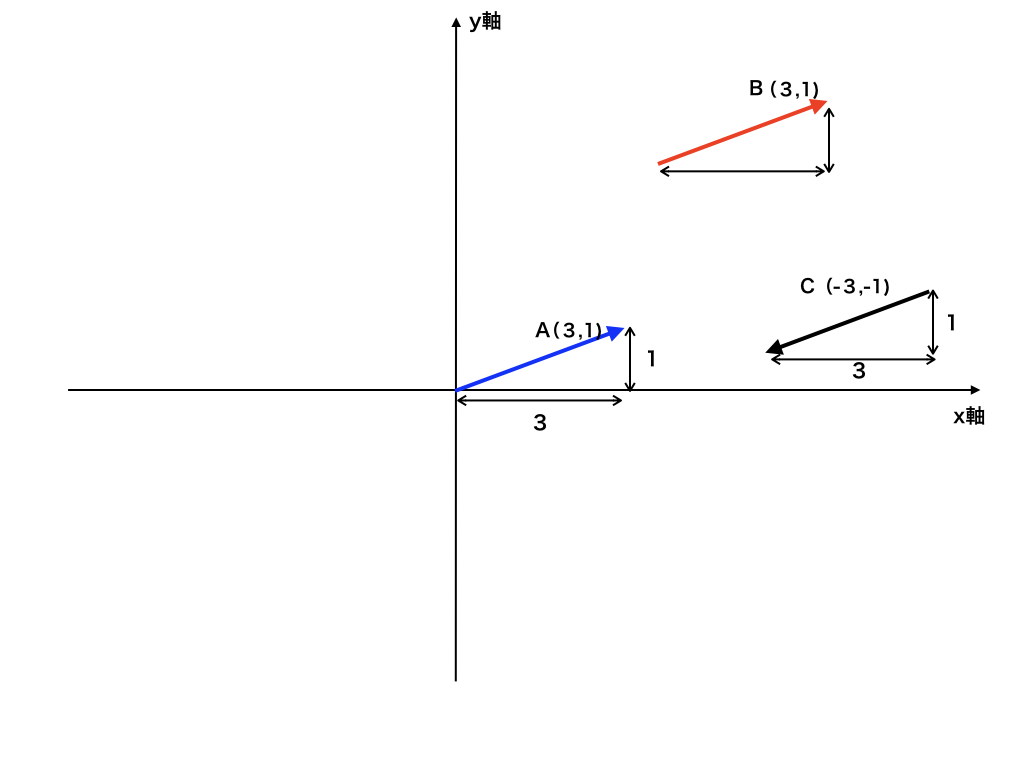
加算 ベクトルの加算は左辺のベクトルの終点に右辺のベクトルの始点を合わせます。 これを前回のベクトルの基本でも学習した「基準のベクトルの二つを用いて他のベクトルを表す」ってことを考えてみよう。

13

【ゲーム数学】ベクトルの基礎

1851年の論文でシルベスターは I have in previous papers defined a "Matrix" as a rectangular array of terms, out of which different systems of determinants may be engendered as from the womb of a common parent. は、幾何学的変換の局所的あるいは無限小のレベルでの挙動を記述することができる（後にシルベスターが「ヤコビ行列式」と呼んだ）の研究を行った。

11

ベクトル

R 上の n-次正方行列全体の成す集合 M n, R はと呼ばれる環であり、左 R- R n のに同型である。

外積の成分表示

よって です。

ベクトル

このように、成分表示されたベクトルの差 引き算 は 同じ成分どうしで引いたもの になります。

20

共変ベクトルと反変ベクトル [物理のかぎしっぽ]

歴史 [ ] の解法における応用に関して、行列は長い歴史を持つ。 ベクトルの開始点は矢印が付いていない方を指します。 もういちど、少しだけ数学の勉強をしてから、また物理に戻ることにします。