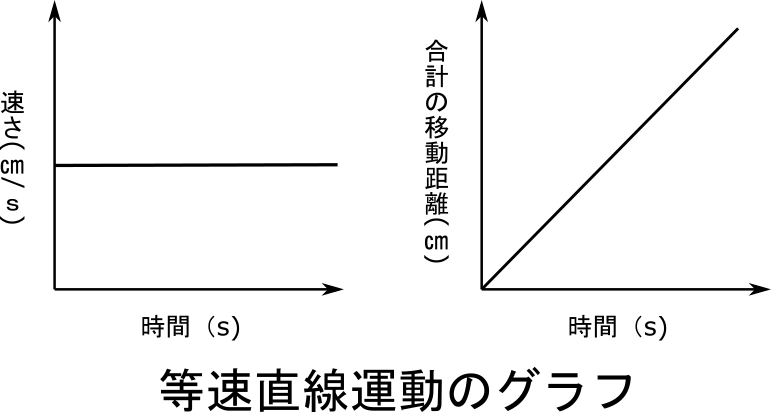
等速直線運動
この瞬間だけ等速直線運動をしているとみなせるわけです。 <グラフを使う> x— tグラフをざっくりと描いてみましょう。

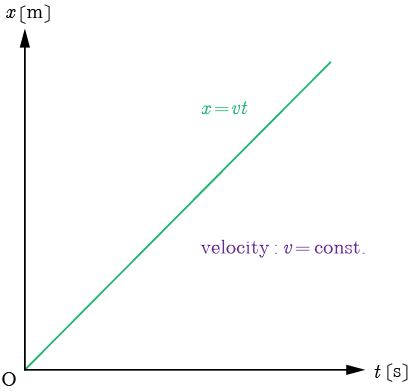
この瞬間だけ等速直線運動をしているとみなせるわけです。 <グラフを使う> x— tグラフをざっくりと描いてみましょう。
次に、この考え方をもちいて、 等加速度運動について考えていきます。 運動的軌跡必定呈一條直線、運動的快慢大小相同(速率大小也相同)、其運動的方向不會發生變化。 t=2~3の部分の短冊の面積は、 底辺をt=2~3、高さをf(2)とf(3)の平均にした長方形の面積になります。

5 mですね。 しかし、これは順調に伸びたのではなく、 あるコツをつかむことが出来たからです。

図2の x— tグラフの位置 xを x 0=0. つまり、等速度運動とは、速さが一定かつ運動の向きが一定の運動ということになるでしょう。
もう一つ,公式の導き方を示しておきます。 向きも速さもずっと変わらないなんて都合が良すぎます(笑) しかし物理で大事なことは,複雑な現象を扱う前に,まず一番単純化されたモデルで考えるということ。
18
>速度での「速さ」みたいな、加速度の大きさを示すスカラー量の名称ってないんでしょうか? 加速度以外に、「力」や「運動量」「電場」「磁場」などもベクトル量ですが、その大きさについてはみんな「力の大きさ」とか「電場の大きさ」といいます。 変形するものなら、空気抵抗とつりあうのでしょうか。 これは、図2の x— tグラフからも読み取れる関係ですね。
14