オイラー の 法則。 オイラー座屈とは？座屈荷重の計算式と導出方法

オイラーの運動方程式

これが，オイラー式と建築基準法上の圧縮許容応力度の関係です。 業績 [ ] 解析学 [ ] スイスの第6次紙幣の10フラン紙幣 （無限小解析）においては膨大な業績があり、の創始以来最もこの分野の技法的な完成に寄与した。

4

オイラーの多面体定理の証明

「おもしろいわね。 この柱は座屈を起こし、yの変形をおこしているとします。 このような現象を座屈といい、座屈を起こした時の荷重を座屈荷重と呼んでいます。

1

オイラーの運動方程式

倍角の公式次は倍角の公式。 ぼくもそう思っていたんだ。

11

オイラーの公式と三角関数の加法定理

参考文献 [ ]• 座屈を知らない人は，完全に直線で均質な材料を完全に軸心に一致する圧縮力を作用させればそれが座屈することはないと考えるものです。 は一般に複素数となるため、平面上の任意の点となる。 おいれる『』・訳、〈数学叢書 第18編〉、1914年。

オイラーの多面体定理の証明

数論 [ ] 以降進展がなかったにおいて、の出現までほぼ一人で研究し続け、や・の拡張など、数々の功績を残した。 両端が固定されている場合は長さが半分になります。

14

オイラーの公式と三角関数の加法定理

そうなるとまた，この問題はますます有名になって，しんけんにこの問題を考える人たちが出てきた。 オイラーの公式とは、eの関数と三角関数をマクローリン展開によって関係づけた式です。 さらにのを積極的に用いて、解析学に限らず数学全分野に大きな業績を残した。

15

一筆書きの秘密

自在継手（ユニバーサルジョイント、モップの先端についてるアレです）や車のタイヤに使われるジョイント（Hinge2Jointと呼ばれたりもします）などがオイラー角の拘束によって実現できます。 また、1737年にはゼータ関数と素数の関係を表すオイラー積の公式を発見し、素数の逆数の和が発散するという新たな結果を得た。

12

オイラーの多面体定理の証明

これじゃあ，いくら考えても一筆書きができないはずだね。 マクローリン展開 指数関数「 e x 」や三角関数「sin x ・cos x 」は、以下のような無限級数で表せることが分かっています。

12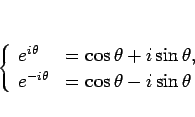

オイラーの多面体定理の証明

参考文献 [ ] ウィキメディア・コモンズには、 に関連するカテゴリがあります。 ただ、「2乗したら－1になる」という性質が1つの数で座標を表したい時などに有用で、主に複素数平面という形で活用されている便利な 「想像上の数」です。

9