オイラー角,固定角,回転行列...
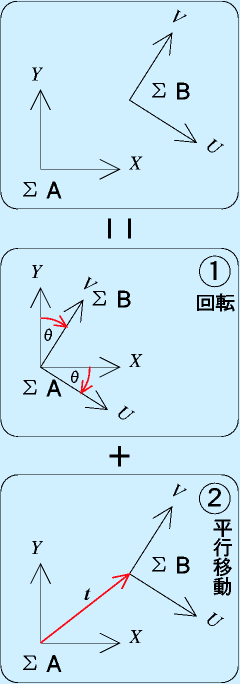
3次元の回転については回転軸がx軸、y軸、z軸と3本あります。 回転量を として成分に書き下すと以下のようになります。

3次元の回転については回転軸がx軸、y軸、z軸と3本あります。 回転量を として成分に書き下すと以下のようになります。

Goldstein, Herbert; Poole, Charles; Safko, John 2001. そして 2 番目は主に Unity での応用を意識しており、3 番目以降は主に航空宇宙での応用を意識しています。
11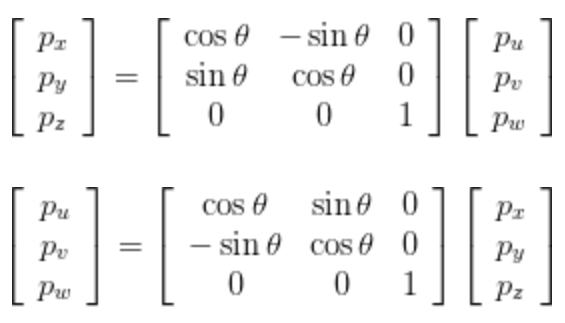
最初の3つがカッコいい? そのような部分や分かりにくい点、曖昧な点を指摘してもらえると、とてもありがたいです。 このとき、パラメータに無駄な自由度があるとそれを抑えるための制約条件を加える必要が出てきますが、制約付きは制約なしに比べて複雑になるので計算コストが高くなってしまいます。
7
1-1. それぞれにメリット・デメリットがあります。 他の軸についても全く同様の計算で示すことができます。
ちなみに2次元平面上の回転の場合は, 回転軸が平面に垂直な方向の1つしか存在し得ないのでこのようなことは起こらず, 最初に右回りに回しても左回りに回しても最終的に同じ結果が得られます. 線形代数の復習から解説されている本で、説明もとても分かりやすい素晴らしい本でした。 特にクォータニオンに関しては, 「なぜこれで回転が表現できるのかわからない」「イメージがしづらい」という意見をよく目にしますので, そのあたりに関する解釈も書いていければと思います. Pythonでのシステム開発依頼・お見積もりはまでお願いします。
2
ジンバルロックなどの計算上の問題を引き起こすこともなく• 自分はこのような事は数日しかしていない全くの初心者なので、間違っているところがあると思います。 up ところで上の定義を見ると• 大きく分けて 2 つの微分方程式があります。 数理的には以下のようになっています。
10