角 運動量。 角運動量演算子

トルク

合わせて読みたい！. モーメント : 回転させる能力を表すベクトル量であり, 向きは回転軸方向である. 2個あるいはこれ以上の角運動量の和を合成角運動量という。 これを、力学的エネルギー保存の法則と言います。 2 角運動量の大きさといずれか一つの成分のみその値を同時に決めることができる。

4

角運動量保存則

質点の慣性モーメント 以上の議論から次のことが言えます。 物体がPで回転運動しているとき、回転の中心からの距離rとPとのを角運動量という。

トルク

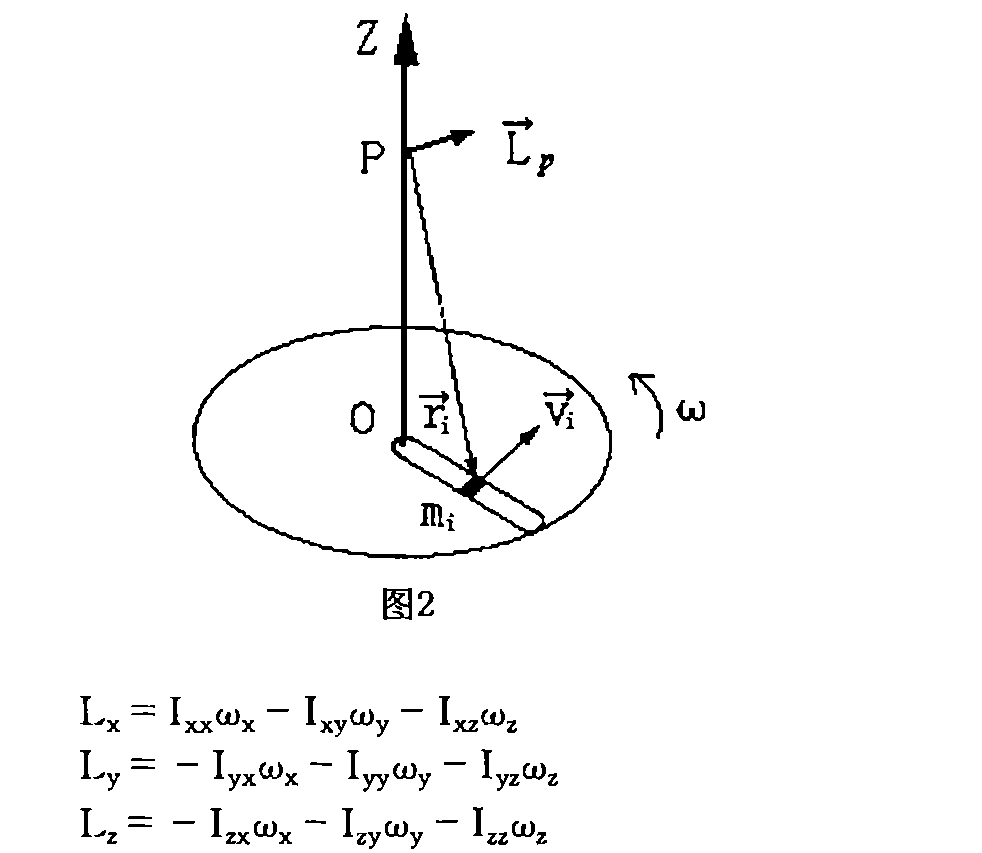
量子的な運動における軌道角運動量のとる値は、マクロな運動（古典力学的運動）の場合と、次の3点で著しく異なっている。 小さなであっても、時間をかければ、角運動量の大きな物体の回転を減速させることができる。 。

角運動量と質点の慣性モーメント

概要 [ ] トルクは、との（）で表される量（）である。

7

角運動量と角運動量保存の法則

この場合、量子的状態は lと mとで表すことができる。 そこで, まずは 物体の回転がどのように引き起こされているのかを学ぶ. 角運動量の時間変化がに相当する。

20

角運動量

量子的状態の場合でも角運動が保存されることが多い。 角運動量と力のモーメント の式の両辺を時間tで微分してみよう。

8

角運動量とは

また、太陽系ではその軌道がほぼ同一面内にあって、各惑星の回転の向きは同じである。 加えるが大きいほど、角運動量の変化は大きい。 にはトルクのプロパティである があります。

8

角運動量と質点の慣性モーメント

との積がである。 したがってベクトル l の成分は次の式で与えられる。

15

角運動量演算子

その後, 回転の勢いを表す量として角運動量を導入し, ある条件が整うことで角運動量が保存されることを学ぶ. そもそも角速度とは速度の角度版，つまり単位時間あたりの角度の変化量を表すのでした。 面積速度一定の法則 : 物体に働く合力が中心力であり, 角運動量保存則が成立する場合には面積速度が一定に保たれる. 物体が大きさを持っていても，どの部分も同じ方向に移動しているわけだから，重心の動きだけを考えれば十分という考え方です。