デルタ関数フーリエ変換

離散データのフーリエ変換とサンプリング定理(標本化定理)の導出【理工数学】│新米夫婦のふたりごと

一方の逆変換は、次のように表せます。丁寧に積分計算ができればラプラス変換は問題ない。

ディラックのデルタ関数とフーリエ級数の関係

手前に余計な係数がくっついてきますが，覚えてあげましょう。

三角関数のフーリエ変換

コンテンツ• 一般の緩増加超関数に対しては積分の形で書いていても積分の意味は持たないことに注意しましょう。

離散フーリエ変換（DFT)

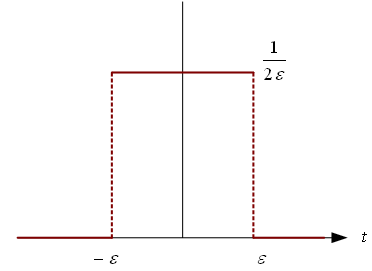
ガウス関数型のフーリエ変換に関する詳細な計算は「」でまとめた。この式が、離散的なデータから元の信号g t を構成する式である。これがGreen関数を用いた微分方程式の解法である。

ディラックのデルタ関数とフーリエ級数の関係

なお、cos関数は偶関数なので、そのフーリエ変換は実部しか持たない。これを逆フーリエ変換すればg t が得られる。

デルタ関数、フーリエ変換についての質問です。多分フーリエ変換...

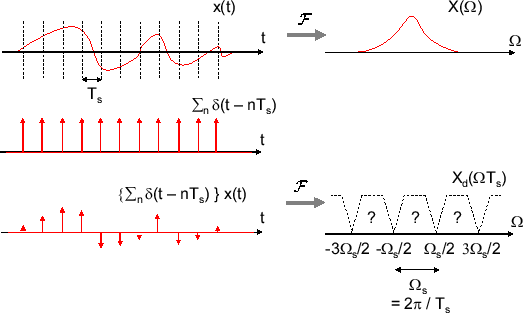
Dはこの積分の値が定まる範囲内で定めます。ディラックのデルタ関数の積分表現が複素フーリエ級数と密接な関係があります。ってのが今回の話になる．結論からいうと，それがフーリエ変換だ．やる夫「級数」が「変換」に変わるんかお．なんか「周期的」かどうかとは全く異質な話に聞こえるお．やらない夫そうかもな．まあその辺は追々理解してもらえばいい．ともかく出発地点はフーリエ級数だ．周期の時間信号を周波数成分に分解するんだった．どんな周波数成分が出てくる? 一方、離散周期信号は、c k を用いて次のように表わされます。